#Technomous #PL

时代逝去的叹息

波斯特断言，存在一些形式系统，我们无法在有限的时间内知道其中某个命题能不能被证明或否证。可以说，他的断言与 10 年后哥德尔的不完备性定理非常相似。那么，为什么在数学史中，“不完备性定理”前面的名字不是波斯特，而是哥德尔呢？因为波斯特虽然在 1921 年得到这个结果，但要等到 1943 年，在哥德尔、图灵、丘奇的黄金时代过去之后，才得以在极省略的篇幅下发表。

他没有跟上时代的节拍。

当时的美国数学界普遍对数理逻辑没有太大的兴趣，波斯特与他的导师凯泽在当时算是异类。要等到第二次世界大战前夕欧洲数学家大幅迁移到美国，这种状况才开始改变。波斯特曾经将他的想法写成上下两篇论文，并且将上篇提交到《数学年刊》（Annals of Mathematics）。但他得到的回复十分令人失望，同行评议的报告对是否应该发表各执一词，而编辑部也没有给出具体的决定。如果没有上篇的理论奠基，那么下篇就仅仅是空谈。

但无人问津还不是最致命的问题。实际上，波斯特根本没有一个实打实的证明。也就是说，他并没有实际证明他的结论，那只是一种推测再加上关于证明的一些想法而已。虽然以我们的后见之明来看，他的结论与想法都是正确的，但他毕竟没有一个能让别人详细检验的证明。

在数学界，证明就是一切。没有证明，即使看上去再确定无误的结论，哪怕拥有再多的间接证据，哪怕是最优秀的数学家的想法，都只能是猜想，而不是定理。要确立一个定理，就必须有一个滴水不漏的证明。这就是数学界的规则。而很不巧，波斯特的研究风格比图灵更依赖直觉，换种说法就是更不严谨。波斯特的直觉足以预见超越时代的结论，但他却没有对应的能力来将他的直觉在当下整理为严谨而有条理的证明。他的雄心壮志超越了哥德尔，甚至超越了图灵与丘奇，但他当时没有足够的工具，也没有足够的能力来完成这样远大的目标。

但也许波斯特多花些时间整理他的思路，就能写出完整的证明来说服数学界。可惜命运没有给他这样的机会。

就在波斯特取得突破之后不久，也许是由于这个结果的冲击性太大，他的心理失去了平衡。而论文未能成功发表更是为这种失常雪上加霜。他患上的是双相情感障碍，患者会在无端愉悦与无故抑郁中震荡。此后十多年，他一直受双相情感障碍的困扰，在数学上毫无产出，申请到的大学教职也因为发作而不得不放弃。这段时期，他只能当一名中学教师聊以糊口。直到 1935 年，他才算是回到了学术界。

从 1921 到 1935，波斯特错过了哥德尔，错过了图灵和丘奇。在他迷惘之时，时代巨轮已经呼啸而过，他错过了数理逻辑的黄金年代。在 1941 年，他写了一篇文章，详细叙述了他此前在逻辑的不完备性方面的工作，投往了《美国数学期刊》。时任编辑赫尔曼·外尔（Hermann Weyl）拒绝了这篇文章：

我毫不怀疑在二十年前你的工作，部分由于它的革命性，没有得到应有的尊重。但我们无法将时针往回拨；在这段时间，哥德尔、丘奇与其他人完成了他们的工作，而美国数学期刊并不是发表历史回顾的地方。

作为编辑，外尔的决定是正确的。探索的前线并不是向迷失者施予救济的地方，历史才是。历史不会忘记这些被忽视的探索者，他们所有的功绩、辛劳与忧伤。波斯特厚厚的研究笔记，就是历史的见证。当时发生的一切将化为铅字，被人们一遍一遍以不同的形式复述，成为集体记忆的一部分。

为传说撰写诗篇，并一直传颂下去，这就是我们能做的一切。

来自Wikipedia

衡量难度的归约

对波斯特来说，错过时代节拍还不算是最大的打击。

当时人们对精神疾病的认识尚浅，没有确实有效的药物，没有确实有效的疗法，一切只能靠摸索。波斯特的双相情感障碍，同样没有标准疗法。当时的想法是，既然发作时出现的是狂喜和抑郁的极端情绪，那么就应该尽量避免这种极端情绪的发生，最好的方法就是限制会导致极端情绪的活动，对于波斯特来说就是数学。他的医生开出的疗法，就是限制波斯特做数学的时间：从下午四点到下午五点，用餐，然后从晚上七点到晚上九点，每天共计三小时。对热爱数学的数学家来说，这简直是能与精神疾病媲美的折磨，就像让美食家用牙签吃最爱的肉酱意粉，我不知道波斯特是如何忍受这种焦灼感的。

幸而波斯特并没有止步不前。他在症状缓解后很快重新投入到数理逻辑的研究中。在图灵刚发表他论述图灵机的论文后，波斯特在对图灵的研究毫不知情的情况下，发表了另一个与图灵机非常相似的模型，现在被称为波斯特机，它与我们常用的计算机更相似，驱动计算的与其说是状态的转移，不如说是语句的执行。他猜想波斯特机的计算能力与 λ 演算相同，这是个正确的猜测，但他当时无法证明这一点。图灵的桂冠并未因此旁落。而波斯特在看到图灵的构造与证明后也心服口服，他的探索再次失去了意义。他后来也考虑过图灵机在多维上的扩展，与后来的“元胞自动机”颇有相似之处。著名的“生命游戏”就是元胞自动机的一个例子。可惜他并没有发表这个想法。

之后，波斯特转到了布尔函数的研究，也就是那些变量与值都是“真”或者“假”的函数。在 1941 年，他发表了一个非常重要的结果：对于函数复合封闭的布尔函数类的分类定理。这些类别构成了一个被称为“格”的数学结构，现在被称为波斯特格。对于当时的研究者来说，波斯特的这个结果虽然很有意义，但研究的对象有些偏门，再加上波斯特典型的那种含混晦涩的行文风格，波斯特格这项成果在当时并没有得到太多的重视。要等到几十年后，人们研究约束满足问题时，波斯特格才重新回到人们的视线中。

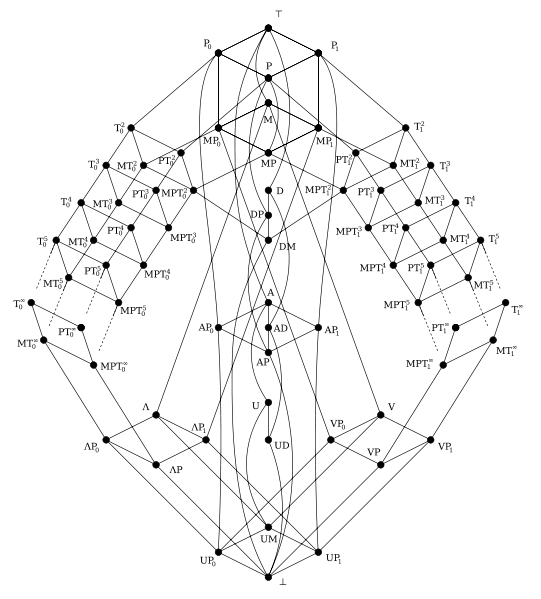
来自Wikipedia

这项结果虽然一开始不太受重视，但毕竟也是正经的研究结果。就这样，通过不懈的努力，波斯特一点一点重新追上了当时数理逻辑的研究潮流，即使每天只能做三个小时的研究。

在 1944 年，波斯特应邀在美国数学协会做了一场演讲。后来他将演讲的内容写成了论文并发表。他自己可能没有想到，这篇论文会成为他最有影响力的论文之一。这篇论文的题目是《递归可枚举的正整数集合与它们的判定问题》（Recursive enumerable sets of positive integers and their decision problems），它希望回答的问题非常简洁：停机问题有多难？有比停机问题容易的不可计算问题吗？

有时候错过时代节拍可能也是一件好事，起码对于波斯特而言，与主流的疏离给他带来了一种与众不同的视角。对他而言，判定问题的计算就是形式系统的推演证明，而形式系统的相互包含是一个非常自然的问题。比如说定义自然数的皮亚诺公理体系，就是一种形式系统，而这个系统中的所有命题都能翻译到集合论的策梅洛-弗兰克（ZF）公理体系中，能用皮亚诺公理证明的数学命题，在翻译后都能在 ZF 中证明。可以说，ZF 体系包含了皮亚诺公理体系。那么，给定两个不同的公理体系 A 和 B，我们自然希望考察它们的包含关系，比如说 B 是否包含 A。也就是说，我们希望知道，是否存在一种方法，能将 A 中的命题翻译到 B 中，并且希望翻译后，在 A 中能证明的命题在 B 中仍然能证明。

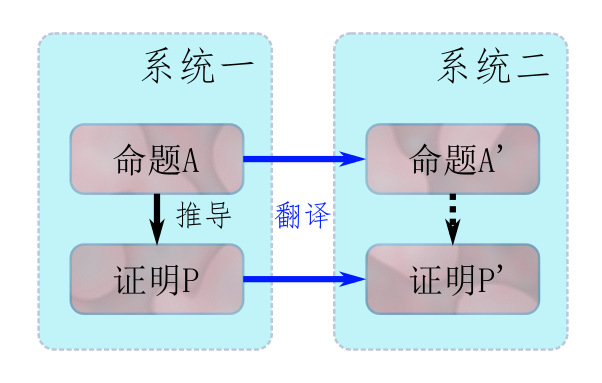
波斯特的另一个优势，就是他之前的研究已经涉及到这样一些具体的翻译问题，只不过用的术语不是翻译，而是归约。从一般的形式系统到正则形式 A，再到正则形式 B，再到一种非常特殊的推演规则，这些都是归约。在关于形式系统不完备性的研究中，波斯特早已自己构造过许多这样的归约。从特殊的归约到一般的“归约”这个概念，对于数学家来说，仅仅是一步之遥。

为了简洁起见，波斯特并没有使用他的正则形式的概念，而是将计算问题表达为一个个由自然数组成的集合。对于数理逻辑学家来说，无论是形式系统、判定问题还是自然数组成的集合，本质上并没有什么不同。形式系统的命题可以用字符串表达，所以可以化为自然数，判断某个命题是否能从公理推演出来，也就相当于判断对应的自然数是否属于可推演命题对应的集合。而一个集合对应的判定问题，就是某个输入作为自然数是否处于这个集合中，所以，指定一个由自然数组成的集合，与指定一个判定问题是等价的。在这个框架下，归约的定义更方便更直观。

归约也有很多不同的种类，它们有强有弱。波斯特在研究形式系统是用到的归约，也就是上面所说的“公理体系之间的翻译”，是其中能力比较弱的一种，又叫“多一归约”（many-one reduction）。而最强的图灵归约在判断 A 中命题的正误时，可以在可计算的范围内任意生成 B 中的命题并得到解答，再从这些任意多的解答中提取结论。能获取的解答数目多了，自然也能解决更多问题，也就是说能力越强。

图灵归约是波斯特研究的最终目标，但它的能力太强，很难研究。所以在 1944 年的这篇论文中，波斯特主要研究的是更简单的多一归约和另一种稍微更强大的“真值表归约”。他证明了，在这两种归约方法定义的难度概念下，存在这样的计算问题，它们是不可计算的，但却比停机问题更容易。也就是说，如果按照这些归约定义的难度来排序，在可计算问题与停机问题之间，存在无数的“中间层级”。从可计算问题到停机问题迈出的这一步，实际上跨过了无数的层级。

波斯特在论文的结尾猜想，对于更强大的图灵归约，这样的“中间层级”也存在，不仅如此，其中有无数个中间层级是计算可枚举的。这并不显然，因为越强大的归约，越能填补不同问题之间难度的差距。比如说，多一归约认为问题 A 比问题 B 要难，但这可能是因为它本身太弱，如果换用图灵归约，也许就能通过多问几个问题得出答案。波斯特关于计算可枚举的“中间层级”是否存在的这个问题，又被称为波斯特问题。

波斯特的这篇论文的新观点和新结果最终引起了美国逻辑学家的注意，他终于获得了作为一个数理逻辑学家应有的赞赏。也许，他并不需要什么救济。

在那场演讲之后，在美国数学协会的聚会上，有个人叫住了波斯特。这个人叫克林，也是一位数理逻辑学家（一些读者可能还记得提出λ演算的丘奇就是他的博士导师）。他对波斯特说，有些东西想让他看看，并将波斯特邀请到了他的家中。

这就是波斯特与克林伟大合作的开端。