计算的极限(三):函数构成的世界
函数构成的世界

丘奇作为图灵在数学上的前辈,思考的问题自然比图灵要深远得多。图灵考虑的问题,仅仅是希尔伯特的可判定性问题,而丘奇当时思考的,是如何重构数学的基础。
当时正是第三次数学危机勃发之际,数学界各路人马对数学基础应该置于何处争论不休。当时公理化集合论刚刚建立,作为新事物,自然有人持观望态度,而丘奇就是其中一位,他觉得自己可以创造一个更好的理论,以此作为数学的基础。与其选择集合与包含这两个概念,他选择了数学中另一个重要的概念:函数。
数学家眼中的函数,比你想像的要广泛得多。在中学数学中,说到函数,自然会联想起它在平面直角坐标系的图像。这是因为中学数学中的函数,大部分情况下不过是从实数到实数的映射而已。而数学家眼中的函数,可能与程序员眼中的函数更相似:它们更像是一个黑箱,从一边扔进去某个东西,另一边就会吐出来另一个东西。
我们并没有限定能扔进黑箱的东西。事实上,将黑箱本身扔进黑箱也是可以的。对这种把戏,数学家们再熟悉不过了,在泛函分析这一数学分支中,数学家们就经常研究一种叫“算子”的数学概念,在某些特殊情况下,就是那些将一个函数变成另一个函数的函数。所以,不去限定能扔进黑箱的东西,似乎也没什么问题。
总而言之,函数就是将一个函数变成另一个函数的东西。那么,要用符号表达这么普遍的函数概念,我们需要什么呢?
首先,就像在方程中我们用 x, y, z 等等符号表示未知数,我们也希望能用符号表示未知函数。我们将这些表示未知函数的符号称为变量。
其次,如果我们手上有两个函数 M 和 N,那么我们自然希望研究函数 N 被函数 M “处理”之后会变成什么。也就是说,既然 M 是一个函数,能将一个函数变成另一个函数,那么 M 会将 N 这个函数变成什么呢?即使不知道具体的过程,我们也希望能表达最后的结果。所以,我们将 N 被 M 处理后得到的结果记为 (M N)。这被称为函数的应用(application)。
最后,也是最抽象的概念,就是函数的抽象(abstraction)。
我们可以用变量 x 来表示未知的函数,自然也可以用 x 来构造更多的函数。比如 (x x) 就表示函数 x应用到自己身上的结果,而((x x) y)就表示将刚才得到的结果应用到另一个未知函数 y 上得到的结果,如此等等,不一而足。如果我们将变量 x 替换成一个具体的函数 f,那么这些包含变量 x 的表达式就会变成包含具体函数 f 的表达式。
也就是说,如果我们有一个包含变量 x 的表达式 M,对于任意一个函数 f,我们可以将它对应到一个新的表达式,记作 M(f),而这个新的表达式是将 M 中的所有 x 替换成 f 所得到的。比如说,如果M=(x x),那么 M(f)=(f f),M((y y))=((y y) (y y)),等等。
一个表达式也是一个函数。我们从表达式 M 出发,可以得到把一个函数 f 对应到另一个函数 M(f) 的方法,而这正是一个函数。也就是说,我们能从一个表达式“抽象”出一个函数。我们将这个函数记作 λx.M,x 是我们所要考虑的自由变量。
【注:在这里,我们只能替换那些所谓的“自由变量”。粗略地说,自由变量是那些之前没有被抽象过的变量。详细的技术细节略显繁复,而且也有办法绕过,所以于此略过。】
从这三点基本要求出发,丘奇开始定义他的 λ 演算。他将他考虑的这些函数称为 “λ项”,而所有的 λ项都可以从以下三种途径构造而成:
- (变量)所有变量 x, y, z, ...都是 λ 项。
- (应用)如果 M 和 N 都是 λ 项,那么 (M N)也是 λ 项。
- (抽象)如果 M 是一个 λ 项而 x 是一个变元,那么 λx.M 也是一个 λ 项。
接下来,丘奇定义了一些 λ 项之间的转换法则。
首先是 α 重命名,这项转换可以使我们在遵循一定的规则下,任意变换 λ 项中的变量名称,而不改变 λ 项本身的意义。也就是说,λ 项中变量的名称无关紧要,无论是 x, y, z 还是苹果、香蕉、榴莲,又或者是小庄、游游、李清晨,项的本质是不变的。
然后是最重要的 β 规约:
在这里,
最后,还有一个 η 变换。它的实质是所谓的外延性,也就是说,如果两个项对所有函数的作用都是相同的话,那么就认为这两个项是相同的。
这么几条简单的法则,就是丘奇的 λ 演算的全部内容。
那么简单的法则,很难想象 λ 演算能表达什么复杂的数学概念,这看起来不过是符号的简单推演而已。但既然同样简单的图灵机中也暗藏玄机,那说不定 λ 演算也有它自己的复杂内涵。
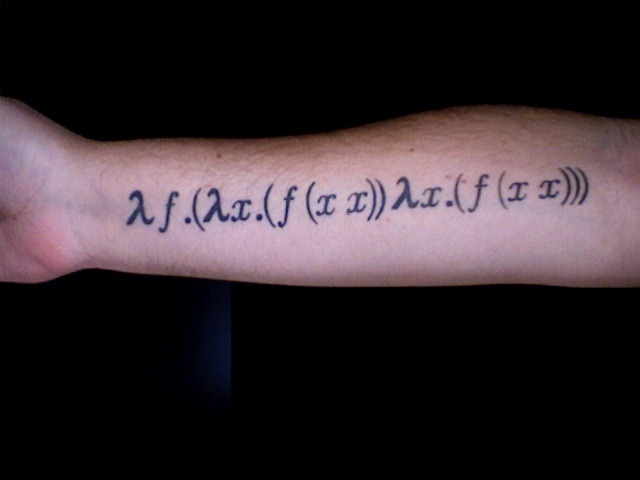
分崩离析的世界
丘奇最初建立 λ 演算的目的,是希望将它作为一种逻辑推理的方法。我们可以将某些逻辑公理表达为 λ 项;对于某个逻辑命题,我们可以先将其转化为 λ 项,再根据 λ 演算的法则将它不断简化,而命题正确与否就蕴含在计算结果之中。
通过这种方法,丘奇成功地在 λ 演算的框架下表达了不少的数学系统。λ 演算看起来是如此的成功,甚至达到了无所不能的程度。
但如果我们还记得哥德尔的教训的话,无所不能有时并不一定是什么好事,因为在数学和逻辑的领域中,对于有意义的逻辑系统,强大的表达能力必然伴随着坚不可摧的限制。如果一个系统无所不能,那么更大的可能是它本身就自相矛盾。就像一个理论,如果对的也好错的也罢,正面反面都能解释得通,那相当于完全没有解释。
果然,几乎在丘奇向学术界展示他的 λ 演算的同时,Kleene 和 Curry 就证明了,作为一个逻辑推理系统,λ 演算在本质上就存在着矛盾,它是不一致的。通过适当地构造一些 λ 项,Kleene 和 Rosser成功地利用 λ 演算找到了一切命题的证明,甚至包括那些错误的命题!一个连错误的命题都能证明的逻辑系统,也就是说一个不一致的逻辑系统,没有任何意义。
值得一提的是,上面这几位后来都成为了数理逻辑界的大人物。Kleene 和 Rosser 是丘奇的学生,而Curry 则师从希尔伯特。我们后面还会讲到这位 Curry 教授,他的事迹之一就是有整整三个不同的编程语言是以他的名字命名的,连中间名都用上了,影响力可见一斑。
事实上,丘奇当初在筑建λ演算之时,就已模糊地认识到了这个问题,但他觉得这只是一种幻象,通过某些适当的限制,就能摆脱这些恼人的问题。但丘奇错了,实际上这是一个本质性的问题。
那么,问题的根源在何处?
我想,读过本系列之前文章的读者应该都猜到了,又是那绕不过去的自我指涉!
但是,自我指涉在什么地方呢?
还记得 λ 项是什么东西呢?它的原型是函数,但不是一般的函数。在定义 λ 项之时,我们允许它将任意的 λ 项转化为另一个 λ 项。既然是任意的 λ 项,那么当然也包括它自己。如果将 λ 项看成程序的话,那又是一个可以将自己当作输入数据的程序。与图灵机不同的是,在 λ 演算之中,根本没有数据和程序之分,一切都是λ项,它们既是程序,也是数据。
λ 演算的能力不止于此。考虑所谓的 Y 组合子:
将它应用到任意一个函数 f 时,我们会得到:
这样不停替换下去,得到的结果就相当于将函数 f 应用到自身任意多次。λ 演算的能力,特别是在自我指涉方面,于此可见一斑。
正是如此强大的表达能力,使得作为逻辑系统的 λ 演算一无所能。如果还记得图灵机是怎么在停机问题上失效的话,实际上利用相似的技巧,对于任意的命题,我们可以构造一个 λ 演算中的证明,无论命题本身是对是错。
后来 Curry 的工作在更深刻的意义上揭示了这一点。他概括了 λ 演算的某些特性,然后证明了对于无论什么逻辑系统,只要它拥有这些特性,那么它必然是不一致的。而这些特性,也恰好是会碍事的那部分自我指涉所需要的。
于是,作为一个逻辑模型,λ 演算一败涂地。
但丘奇没有就此止步。虽然 λ 演算不能如他所愿成为数学的推理基础,作为一个计算模型似乎倒也不错。我们可以将一个计算过程看成函数,将输入数据转化为输出数据的函数。于是丘奇将“可有效计算”定义为“可以用 λ 演算表达的函数”。这时,自我指涉的特性就成为了不可多得的优点,因为这实际上说明 λ 演算有强大的计算能力。利用自我指涉的特性,通过相似的构造方法,丘奇同样解决了希尔伯特的可判定性问题,得到了与图灵相同的结论。
丘奇在构想 λ 演算之时,瞄准的是更为基本的数学基础模型,但它却成为了可计算性的模型,真可谓“无心插柳柳成荫”。这就是图灵看到的那篇论文的由来。
不难想象图灵当时读到这篇论文时的心情。如果将数学比作攀山,当你千辛万苦登上一座处女峰,却蓦然发现山顶已经插上了别人的旗帜,你大概会觉得一切都似乎失去了意义。
但数学毕竟不是攀山,不同的路径可能有不同的景致,要论高下为时尚早。况且要比较两者,要先知道两者解决的到底是不是同一个问题。虽然图灵和丘奇解决的都是同一个问题,但他们对“可计算性”各自做了不同的假定。图灵认为“可计算的问题”就是图灵机可以解决的问题,而丘奇则认为那应该是 λ 演算可以解决的问题。
问题是,图灵机和 λ 演算这两个计算模型,它们解决问题的能力一样吗?两种视点下的可计算性,到底是殊途同归,还是貌合神离?