#Technomous #PL

所有机器的机器

图灵机非常简单，只要明白了它的运作过程，任何一个受过足够训练的计算机系本科生都可以写出一个模拟图灵机运行的程序。只消输入状态转移表和纸带的输入内容，程序就可以一步一步模拟相应的图灵机在纸带上爬来爬去的过程。对于一些熟悉图形编程的程序员来说，做个模拟动画也问题不大。即使不用计算机，靠人手一步步操作，也是一件小孩子也能完成的事。图灵机就是这么简单的一种机器。

虽然看上去简单，但实际上图灵机能做的事情远远超出一般的想象。只要有足够长的纸带和足够好的耐心，今天的电脑能做的计算，一台精心设计的图灵机也能完成。诀窍在于，电脑中的电路是有限的，电路的状态也是有限的，我们可以用图灵机去模拟电脑中的电路状态。只要有足够长的纸带，那就可以模拟出足够大的寄存器、内存和硬盘；而 CPU 中的电路，虽然所有可能的状态极其多，但终究是有限的，可以用图灵机模拟，虽然这台图灵机的状态转移表将会有着令人头痛的大小，以及令人偏头痛的复杂程度。但是，从原则上来说，用图灵机模拟一台电脑是完全可能的，虽然每次“读写内存”时，读写头都需要花长得令人咋舌的时间在纸带上来回奔波。

也就是说，从原则上来说，只要配备适当的输入和输出设备，以及极其好的耐心，我们完全可以用图灵机上网、玩游戏甚至执行自己写的程序。特别地，存在一台特定的编写程序专用的图灵机 T，我们可以在纸带上写程序，将它输入到 T，然后 T 就能执行这个程序。那么，如果我们将方才本科生写的那个可以模拟任意图灵机运行的程序（暂且把它称为程序 P），写在纸带上输入到 T 中，让 T去执行的话，原本的机器 T 就摇身一变，变成了一台可以根据输入的状态转移表来模拟任何一台图灵机的图灵机。

更精确地说，因为程序 P 的长度是有限的，我们可以将它直接写进原来机器的状态转移表，得到一台新的机器 UTM。UTM 会在纸带上读取两样东西：一台图灵机 M 的状态转移表的二进制编码，以及作为 M 的初始输入的纸带数据。然后，UTM 会根据 M 的状态转移表和初始输入数据，在纸带上模拟 M 的运作过程。换言之，UTM 是一台可以模拟任何图灵机的图灵机。它是所有机器的机器，所谓的通用图灵机（Universal Turing Machine）。当然，通用图灵机并不是唯一的，只要一台图灵机能完成根据状态转移表模拟任意图灵机的任务，它就是通用图灵机。

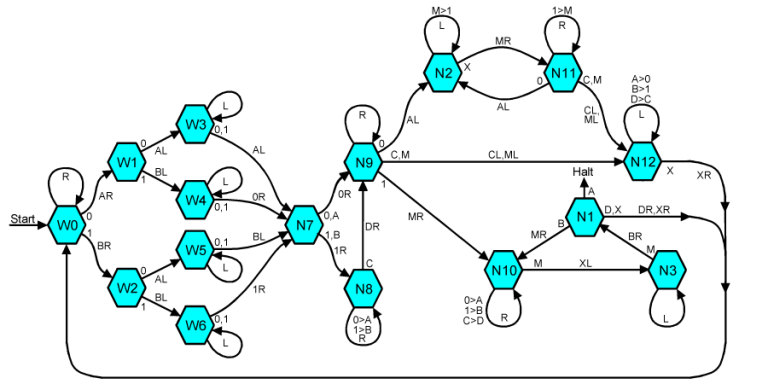
一台通用图灵机，数据具体格式请参见来源：A Universal Turing Machine For The GoL Turing Machine

通用图灵机的想法，在如今这个计算机泛滥的时代，似乎并不新鲜。但在图灵的 1935 年，电子计算机甚至仍未问世，机械计算机还只能执行内设的一套指令。即使是 Charles Babbage 和 Ada Lovelace 的超越时代的设想，其中执行外部程序的概念也相当含混不清。在这种历史背景下，要归纳出通用图灵机这个概念，本身就需要极为丰富的想象力，而且这种图灵机是否存在，这是个远非显然的问题。而图灵不仅设想到了这个概念，而且正确地判断出它的存在性，这需要何等非凡的直觉！

但单纯的直觉终究不能令人信服，数学家讲究的是逻辑和证明。而要证明通用图灵机的存在，最直接的方法莫过于直接给出一个通用图灵机的实例。这并不简单，如果读者想尝试一下的话，我建议先尝试构造一个能做二进制加法的图灵机。为了降低难度，可以假设纸带上有第三种符号，表示空白，但即使如此，要构造一个能做加法的图灵机，远比想象中的困难。可想而知，通用图灵机的构造肯定更为复杂繁琐。即使是图灵，他在一开始给出的构造也是有问题的，而这些问题甚至在后来的勘误中也没有成功修正。比构造更麻烦的是证明给出的图灵机的确是一台通用图灵机，在图灵解决希尔伯特可判定性问题的论文中，有关通用图灵机的构造和证明占了相当大的篇幅。这部分非常繁复琐碎，而且其中还有错误，如果细细研读的话，绝对有诱发剧烈偏头痛的危险。

幸运的是，无论细节多么复杂，图灵的想法还是被逻辑学家们接受了。一旦领会到图灵机的能力，接受了通用图灵机的构想，再检查几个能完成基本任务的图灵机之后，大部分数学家都会认为通用图灵机的确存在，尽管他们并不一定会细看图灵的详细构造。而现代电子计算机的发展，更是验证了通用图灵机的存在：每一台电脑都相当于一台通用图灵机。

通用图灵机的存在，从侧面说明了图灵机这个计算模型的强大之处：图灵机作为一类机器，其中一个特例就可以模拟整个类别中的任意一台机器，宛如能折射大千世界的一滴水珠。但在这种强大的背后，隐隐也暗藏着不安定的因素。哥德尔不完备性定理告诉我们，有时候越强大的数学理论，因为能表达的概念太多，甚至连理论的命题和证明都能表达，反而会导致不能被证明的真命题的存在。如果一个系统足以描述它自己，那魔法般的自指将是不可避免的。图灵机如此强大，它的其中一台就可以模拟所有图灵机，会不会导致不能用计算来回答的问题存在呢？

很不凑巧，答案是会。

无法计算的问题

在哥德尔不完备性定理的证明中，哥德尔构造了一个描述了本身不可证明性的自指命题，通过这个命题完成了他的证明。要想照葫芦画瓢的话，那些关于图灵机本身的问题，将会是很好的候补。

关于图灵机，最简单的问题是什么呢？回想一下图灵机的运作过程，一台图灵机从初始状态开始，根据纸带上的内容，一边不断变换状态，一边更改纸带的内容，如此往复永无休止，除非它遇上了表示停机的那个状态，才能从这机械的计算过程中跳出，获得静息的安乐。一个自然的问题是：一台图灵机什么时候会停机呢？

更严格地说，会不会停机并不是图灵机本身的属性，它跟纸带的初始输入也有关系。对于同一台图灵机，不同的纸带输入也可能导致不同的结果和行为。比如说，我可以设计一台图灵机，它的任务只有一个：一步一步向右移动，寻找输入中的第一个 1。如果输入纸带上全是 0 的话，那么，这台图灵机自然不会停止；但只要纸带上有一个 1，那么它就会停止。所以，真正严谨的问题是：给定一台图灵机 M 以及一个输入 I，如果我们将 I 输入 M，然后让 M 开始运行，这时 M 是会不停运转下去，还是会在一段时间后停止？我们将这个问题称为停机问题。

初看起来，停机问题并不难。既然我们有通用图灵机这一强大的武器，那么只需要用它一步步模拟M 在输入 I 上的计算过程就可以了。如果模拟过程在一段时间后停止了，我们当然可以得出“M 在输入 I 上会停止”这个结论。问题是，在模拟过程停止之前，我们不可能知道整个计算过程到底是不会停止，它可能会在 3 分钟后停止，可能要等上十年八载，更有可能永远都不会停止。换句话说，用模拟的方法，我们只能知道某个程序在某个输入上会停止，但永远不能确定那些不停止的状况。所以说，单纯的模拟是不能解决停机问题的。

实际上，停机问题比我们想象中要复杂得多。

举个例子，我们可以编写一个程序 GC，它遍历所有大于等于 6 的偶数，尝试将这样的偶数分成两个素数的和。如果它遇到一个不能被分解为两个素数之和的偶数，它就停机并输出这个偶数；否则，它就一直运行下去。用现代的工具编写 GC 这样的程序，对于计算机系的学生最多只能算一次大作业；用图灵机实现的话，也不是什么极端困难的事。然而，GC 是否会停止可是牵涉到了哥德巴赫猜想。如果哥德巴赫猜想是正确的，每个大于等于 6 的偶数都能分解为两个素数之和的话，那么 GC 自然会一直运行下去，不会停机；如果哥德巴赫猜想是错误的话，必定存在一个最小的反例，它不能分解为两个素数之和，而 GC 在遇到这个反例时就会停机。也就是说，GC 是否永远运行下去，等价于哥德巴赫猜想是否成立。如果我们能判定 GC 是否会停止，那我们就解决了哥德巴赫猜想。

数学中的很多猜想，比如说 3x+1 猜想、黎曼猜想等，都可以用类似的方法转化为判断一个程序是否会停止的问题。如果存在一个程序，能判断所有可能的图灵机在所有可能的输入上是否会停止的话，那么只要利用这个程序，我们就能证明一大堆重要的数学猜想。我们可以说，停机问题比所有这些猜想更难更复杂，因为这些困难的数学猜想都不过是一般的停机问题的一个特例。如果停机问题可以被完全解决，我们能写出一个程序来判断任意图灵机是否会停机的话，那么相当多的数学家都要丢饭碗了。

停机问题如此复杂，机械的计算看起来没有足够的力量来完全解决它。停机问题似乎是不可计算的。但要想严格证明这个结论，似乎仍要求助于深藏在图灵机之中，那魔法般的自指。