符号与机器(三):图灵机的解释
能不能找到一个算法来决定任意一个整系数的代数方程是否有整数解 — — 希尔伯特第十判定问题

前面讲了代数系统,以及基于代数运算抽象出来的逻辑系统。那么计算是如何自动化的?我们现在讲一讲什么是“图灵机“。
为了证明不存在希尔伯特在第十判定问题中所期望的算法,图灵开始关注包括人在内的整个运算行为过程。
图灵通过把非本质的东西丢掉,将整个计算过程局限在了少数非常简单的操作上。现在我们试着从一个都熟悉的东西入手,来探究图灵的思考过程。
我们现在开始解构两个三位数相乘的运算过程。通常人工的乘法步骤如下,
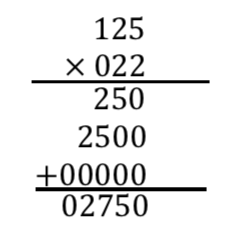
通过观察整个运算过程,可以发现,我们每一步运算都只是对当前的两个数字进行运算操作,并不关心其他数字。除了需要知道当前运算到哪一个数字之外,我们还需要知道当前是否有进位,当前的运算符号等额外的人为记忆的东西。
现在把整个算式平铺放到一条带网格的纸带上,

那么整个运算过程和之前并没有太大不同。想象我们可以操作纸带前后移动,
第一步:

我们首先把纸带分别依次移动到第3、4、6个网格,得到的暂存数据如下:
当前运算数字:5、2
当前进位:0
当前符号:✖️
经过运算,并将运算结果写到第11个网格中,并更新进位为1。
第二步:

继续把纸带分别依次移动到第2、4、6个网格,得到的暂存数据如下:
当前运算数字:2、2
当前进位:1
当前符号:✖️
经过运算,并将运算结果写到第10个网格中,并更新进位为0。
第三步,依次同上。
就这样依次运算下去,我们就可以在有限的步骤内,完成计算。从这个简单的乘法例子我们可以得到:
1)在每一步中,只需要关注当前的两个数字
2)每一步采取的行动,仅仅取决于当前的乘法、加法、进位值
更进一步,从这个简单的乘法运算,我们可以提取出任何数学运算的本质特征:
1)在每一步中,只需要关注少数符号
2)每一步采取的行动,仅仅取决于当前的运算符号、计算人当前的记忆状态
运算行为过程中的人,是完全可以由机器取代的。这就是图灵最初给出的,自动运算机器的抽象逻辑归纳,也是用来证明判定问题不存在算法的方法:如果一个问题无法用图灵机来完成,那么可以说,没有任何算法程序可以解决这个问题。也就是说,凡是能用算法方法解决的问题,也一定能用图灵机解决。
其实图灵机是一个非常简单的模型,至于图灵是如何想到的,也许只有他知道吧。而我们,需要站在他的肩膀上继续前行,相信只要我们努力思考,总能找到出路。