计算的极限(二):自我指涉与不可判定
矛盾的自我指涉
在现实中,证明某种东西不存在是非常困难的。要证明某种东西存在,只要举出一个例子就可以了;但要证明某种东西不存在,就要想办法排除所有的可能性,而在现实生活中,这几乎是不可能的。所以,只要能排除那些比较主要的可能性,任务就算完成。但在数学中,情况大不相同:通过形式逻辑的方法,我们可以确实地证明某种数学对象不存在。这都要归功于数学那彻底的抽象化和形式化。
数学家在证明某个数学对象不存在的时候,经常会来一招“欲擒故纵”:首先假设它存在,那么它必然具有某些特定的性质,再利用这些性质,用严密的逻辑推理引出一个不可能的结论。既然结论是不可能的,而逻辑推理又没有问题,那么一定是推理的出发点出了差错:作为推理基础的那个东西,其实并不存在。这种证明方法,就是反证法。
现在,我们尝试用反证法证明停机问题是不可计算的。
按照反证法的格式,我们先反其道而行之,假设停机问题是可以计算的。根据定义,这说明存在一台图灵机 P,使得向它输入某个图灵机 M 的状态转移表编码 <M>,以及初始输入 I,图灵机 P 就能在有限步运算内,判断出机器 M 在输入 I 上是否会停止。
接下来,我们将要用图灵机 P 构造一个逻辑上不可能存在的结构,这将是证明的关键。
我们来考虑一个新的图灵机 R,它的输入是某个图灵机 M 的状态转移表编码<M> 。图灵机 R 先“调用”图灵机 P,判断图灵机 M在初始输入<M> 上是否会停止。用现代的计算机语言来说,就相当于调用函数P(<M>,<M>)。如果图灵机 P 得出的结论是机器 M 在输入<M>上停止的话,图灵机 R 接下来就会进入死循环;否则,如果机器 M 在输入<M>上不会停机的话,图灵机 R 就停止。
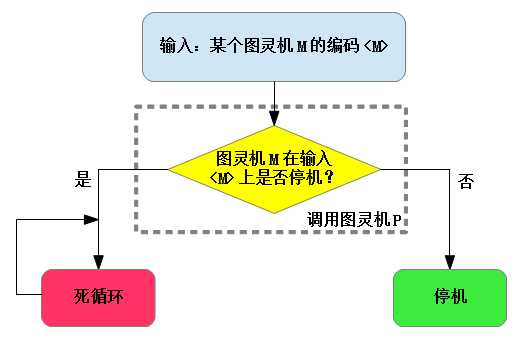
图灵机 R 的构造有两个奇怪之处。
首先,在图灵机 R 的运作中,它尝试判断一台图灵机 M 在它自身的编码<M>上的运作情况。此时,图灵机 M 不仅是程序,同时也是数据。这提醒我们,其实程序和数据没有实质的区别。程序只是一种特殊的数据,能够被分析、整理、改写。
事实上,我们每天都在使用处理程序的程序。比如说杀毒软件,其实就是一种扫描程序的程序。它检查每个程序的内容,判断程序中有没有威胁计算机安全的恶意代码。用杀毒软件扫描它自身,实际上就是让这个程序运作在它自身的代码之上。我们也可以用记事本打开记事本的程序本身,或者用压缩软件打一个包含它程序本身的压缩包。这些例子都说明了一个道理:程序就是一种数据。正因为程序就是数据,我们才得以完成图灵机的自我指涉。
其次,在图灵机 R 的构造中,如果 M 在<M>上停机,那么 R 就不停机;如果 M 在<M>上不停机,那么 R 就停机。这就是说谎者悖论的翻版:它的行为要与自己的判断相悖。
这样,我们就凑齐了说谎者悖论的两个要素:自我指涉和自我否定。剩下的,就是如何将这两个要素组合在一起,引出不可调和的矛盾了。
为了引出矛盾,我们来考虑图灵机 R 在自己的编码<R>上的运行情况。
如果 R 在<R>上停机的话,R 必定没有进入死循环。所以,在调用图灵机 P 时,得到的必然是“图灵机 R 在输入<R>上不会停机”,才能避免死循环。但图灵机 P 的这个结论不符合我们的假设,出现了逻辑矛盾,所以 R 不可能在<R>上停机。
如果 R 在<R>上不停机的话,因为图灵机 P 必定在有限时间内完成计算,所以 R 必定进入了死循环。而 R 进入死循环的先决条件是,在调用图灵机 P 时,得到的是“图灵机 R 在输入<R>上停机”。而图灵机 P 的这个结论,同样不符合我们的假设。由于同样的逻辑矛盾,R 同样不可能在<R>上不停机。
所以,根据严密的逻辑,我们构造的图灵机 R 在自己的编码<R>上,既不可能停机又不可能不停机,这是不可能的。另一方面,我们的逻辑推理也是没有问题的。尽管多么不情愿,剩下的可能性只有一种:我们假设的那个能完美解决停机问题的图灵机 P,根本不存在!也就是说,停机问题是不可计算的。
这个结论,我们称之为停机定理。以上的论述,作为停机定理的证明远远不算严谨,还有很多细枝末节需要填充。但这些细节都是技术性的,并不妨碍主要的思想:矛盾的自我指涉。
停机定理的证明,一如哥德尔不完备性定理的证明,核心是化了妆的说谎者悖论。图灵机的能力如此强大,一台通用图灵机就可以完成一切图灵机的工作,将所有图灵机作为数据处理。也正因如此,图灵机不能解决某些牵涉它自身的问题,否则总会存在一些自我否定的“说谎者”,利用能解决牵涉自身问题的那些图灵机,完成被逻辑所禁止的,致命的自我指涉。图灵机的能力,在必然的逻辑推演下,同时也成了它的枷锁。
不可判定的重复
实际上,图灵一开始并没有证明停机定理。他证明的是:不存在这样的程序,能判断任意图灵机是否会至少打印出一个 1。这里的“1”可以换成任意的符号。这个证明的方法要稍复杂些,不过本质上仍然是通过自我否定与自我指涉来制造悖论。而事实上,许多(但不是所有)有关图灵机的问题,都能用同样的方法被证明是不可计算的。这样,图灵手上就有了一套不可计算的问题,可以开始考虑希尔伯特的问题了。
我们回顾一下希尔伯特的问题。哥德尔证明了,所谓的“一阶谓词演算”是完备的。也就是说,在这个数学系统中,每个真理都能被证明,“真”和“能被证明”这两个概念是一致的。希尔伯特的可判定性问题是:是否存在一种计算过程,可以在有限步运算内,判断在这个完备的数学系统中每个命题的真假?
一阶谓词演算作为数学系统,在能力上实在是比不上数学家们常用的逻辑系统:它连自然数都不能很好地定义。但图灵发现,这个稍弱的数学系统已经足以表达图灵机的运行过程。对于每个图灵机 M,通过巧妙然而机械化的操作,图灵都能构造出一阶谓词演算中的一个命题 U(M),使得 U(M) 成立当且仅当图灵机 M 会至少打印出一个 1!也就是说,命题 U(M) 是否为真与图灵机M的运行过程息息相关。
剩下的证明就如同探囊取物了。如果希尔伯特的可判定性问题是可以计算的话,必定存在一台图灵机 H,可以在有限时间内,判断每个命题的真假。对于一台图灵机 M,我们要知道它是否会至少打印出一个 1,可以先机械化地计算出与 M 有关的命题 U(M),然后用图灵机 H 去判断 U(M)的真假,从而判断图灵机 M 是否会至少打印出一个 1。也就是说,利用图灵机 H,我们可以用计算回答一个不可计算的问题,而这是不可能的。所以,图灵机 H 并不存在,希尔伯特的可判定性问题的答案只有三个字:不可能。
希尔伯特的期望,又一次化为泡影。逻辑弄人。
图灵确信自己解决了希尔伯特的判定问题后,很快将他的想法写成了论文,它的题目是:
《论可计算数,及其在可判定性问题上的应用》(On Computable Numbers, With an Application to the Entscheidungsproblem)
他将论文交给了数理逻辑课的纽曼教授。这篇论文在纽曼教授的桌上放了几个星期。当教授终于有时间细读图灵的论文时,一开始根本不敢相信希尔伯特的问题竟然能通过对如此简单的机器的论证而解决,但无懈可击的逻辑论证最终战胜了怀疑。这无疑是划时代的工作,最终埋葬了希尔伯特的宏伟计划。
但正当纽曼教授联系各方,想办法发表图灵的论文时,从大西洋彼岸的普林斯顿,寄来了一篇论文:
《初等数论中的一个不可解问题》(An unsolvable problem of elementary number theory)
它的作者是丘奇(Alonzo Church),普林斯顿大学的一位年轻数学教授,当时在数理逻辑这一领域已经小有名气。而这篇文章的最后一句话是:
In particular, if the system of Principia Mathematica be ω-consistent, its Entscheidungsproblem is unsolvable.
(特别地,如果《数学原理》中的系统是 ω-一致的话,它的可判定性问题是不可解的。)
对于图灵来说,这绝对不是一个好消息,因为这与他的结果是一样的。
那么,丘奇又是如何得到这个结论的呢?