计算的极限(十):无限绵延的层级
交错的存在所有
波斯特在演讲中谈到了关于自然数集之间归约的问题,而克林当时也正在研究类似的问题:用不同的逻辑公式定义的自然数集,它们是否不同,又有什么不同?如果在一个关于自然数的逻辑公式 P(x) 中,只有一个自由变元 x,那么,使这个公式成立的所有值组成的集合就是 P(x) 定义的自然数集。每个自然数集又对应一个判定问题:某个自然数 n 在这个自然数集中吗?
用这种方法定义的自然数集,它们有着什么样的性质呢?
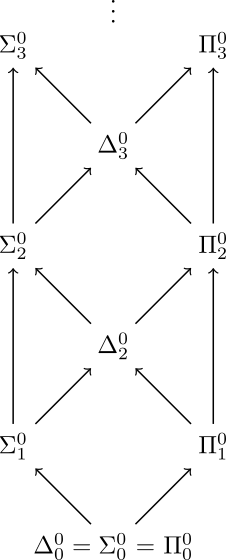
我们知道,在逻辑公式中,除了我们熟悉的变量和加减乘除,还有一种符号叫“量词”。量词分两种,存在量词
我们知道,所有一阶逻辑的命题都可以将所有量词整理到命题的开头,对于现在的数学系学生来说,这只不过是一道小小的练习题。所以,我们可以假定所有命题都有着这样的形式。按照开头量词的具体形式,克林将所有有关自然数的命题分成了无穷个类别。没有量词的命题被称为零阶命题,而有量词的命题,它们开头必定由存在量词和全称量词交错组成,这样交错的段数,就是命题的阶数。对于一个 n 阶命题,如果它的开头是存在量词,我们就称它为 n 阶存在命题,反之则是 n 阶全称命题。根据这个定义,我们能轻易看出一个性质:n+1 阶存在命题,其实就是 n 阶全称命题开头加上一些存在量词得到的。而在这个性质中,将“存在”和“全称”两个词反过来,它仍然成立。
(注:在关于自然数的逻辑命题中,还有一种特殊的量词,被称为“有界存在量词”。在 n 阶命题的定义中,我们忽略这些有界存在量词。)

来自Wikimedia
我们来看一个实际的例子。著名的哥德巴赫猜想说的是,对于每一个大于等于 4 的自然数,都能被写成两个素数的和。对于某个特定的偶数 2n+4,我们能将“2n+4 能写成两个素数的和”写成以下的逻辑命题:
这个命题是一个 2 阶全称命题,因为它的量词分两截,而开头是一个全称量词。
克林考虑了所有这些类别的命题能定义的自然数集。他将 0 阶命题定义的自然数集组成的集合称为
也许不出大家的意料,克林证明这一切的方法,仍然是康托尔的对角线法。他定义的这个层级,今天被称为算术层级(Arithmetic Hierarchy),是数理逻辑中的一个重要概念。
克林的这项工作,给了波斯特非常大的启发。这是为什么呢?
我们先来看看
那么,
那么,不可计算的问题,比如说停机问题,它又在哪个层级呢?可以证明,停机问题相关的命题可以在更高的
波斯特之前的工作聚焦于难度处于可计算问题与停机问题之间的问题,但克林的工作促使他将目光投向另一个方向:难度比停机问题更高的计算问题,在图灵归约之下,它们有着怎样的结构?
无法触及的世界
我们先复习一下图灵归约的概念:考虑一台谕示机 M,假设它带有问题 A 的谕示,如果它能解决某个问题 B,那么我们说问题 B 能被图灵归约到 A,记作
图灵等价是一种等价关系:如果 A 图灵等价于 B,而 B 图灵等价于 C,那么 A 也图灵等价于 C。我们可以将那些相互之间图灵等价的问题归为同一类(数学术语是等价类)。这些类别,被称为“图灵度”,它们之间可以通过图灵规约来比较难度,可以说,在同一个图灵度中的判定问题,在图灵规约的意义下,难度都是相同的,而带有其中任意一个问题的谕示,给谕示机带来的能力都是相同的,可以互相置换。
那么,这些图灵度到底看起来是什么样子的呢?
显然所有的可计算的判定问题都是图灵等价的,因为“可计算”的定义就是“存在图灵机可以解答”,既然一般的图灵机足以解答,那么任意的谕示机当然也可以。因为这些判定问题对于图灵机来说过于简单,不需要谕示就能完成,所以谕示的内容反而变得不重要,带有一个可计算谕示与没有谕示,对于图灵机来说是一样的。同样,任意的可计算判定问题都能图灵规约到任意的判定问题。可以说,在图灵规约的框架下,可计算判定问题就是那些最“简单”的问题,它们组成了最“容易”的图灵度,被记作
那么,停机问题又如何呢?图灵证明了任意的图灵机都不能解决停机问题,同样,带有一个可计算谕示的谕示机当然也不能解决,因为这样的谕示机与一般的图灵机的计算能力是相同的。也就是说,停机问题不能规约到任何一个可计算的判定问题,也就是说,停机问题比那些可计算的问题要严格地难,或者说,停机问题与可计算问题不在同一个图灵度。所以,我们至少有两个图灵度,一个是可计算的
那么,如何构筑更难的问题呢?
图灵在他的博士论文中发现,在停机问题不可计算的证明中,将所有的“图灵机”全部换成“带有‘数论问题’的谕示机”,其他部分不易一字,得到的证明仍然正确。从而他证明了所谓的“数论问题”并不包含所有的计算问题。在这里,图灵选取了“数论问题”这个谕示,但实际上,无论选取什么计算问题的谕示,将它代入原来的证明,得到的证明仍然成立。也就是说,对于任意的判定问题A,带有问题A谕示的谕示机是否会停机,这个判定问题是不能用带有问题A谕示的谕示机解决的。如果问题A是某个图灵度
(注:顺带一提,类似这样可以将“图灵机”换成“谕示机”的证明被称为可相对化的证明(relativizable proof)。这个概念的变体在 P 与 NP 问题中占据着重要的地位。更精确地说,在所谓的“多项式归约”的概念下,解决 P 与 NP 问题的证明不可能是可相对化的。这个结论又被称为“可相对化障碍”。)
这就是波斯特构筑越来越难的图灵度的方法。对于某个图灵度
实际上,波斯特的图灵度层级与克林的算术层级之间的联系,比我们想象中的更深刻。我们定义
但图灵度层级实际上比算术层级延伸得更远。在算术层级的定义中,第n层是由那些拥有n段不同量词的命题构成的,因为命题的长度有限,所以n只能是自然数。在这里,n表达的是数量,也就是基数。但在图灵度层级中,定义的方法则是通过图灵跳跃,是一种顺序关系。在
也就是说,尽管人力能及的只有可计算的问题,但通过逻辑推演,我们能认识到,在那些我们无法解答的问题中,竟然还存在着一个精巧的结构。而正是波斯特,向我们首次展示了这个无法触及的世界。

无限绵延的层级
波斯特很快就将他的部分发现以摘要的形式发表在 1948 年的《美国数学学会通报》上。克林读到了这篇摘要,自然为波斯特的新发现而兴奋,但他对这份摘要并非毫无意见。
数学家尽管做的都是数学,但他们的处事方式却是各式各样。在提笔写作方面,有的数学家勤于下笔,每获得了新的结果,就会很快写出论文,并通过期刊或者私下流通预印本的形式让同行尽快知道他的结果;有的数学家却惜字如金,即使有了一整套新结果,也记录了相关的定理和证明,但却迟迟不肯下笔,也许是希望更好地打磨这些结果。著名数学家埃尔德什和欧拉是前者的典型代表,两者分别是数学史上发表论文第一和第二多的数学家。而同样著名的高斯和怀尔斯则是后者的典型代表。高斯是个完美主义者,他希望他的著作中毫无瑕疵,“将所有的脚手架去掉”,于是他发现的结果往往在抽屉里一躺就是几年,直到高斯终于满意他的写作,或者别的数学家再次发现这个结果为止。而怀尔斯独自一人在八年时间内钻研,完成费马大定理的证明主体,这早已传为佳话,被认为是怀尔斯坚韧性格的证明。这些不同的风格,也许在不同的环境下有着不同的适应性,但却没有绝对的对与错之分。
波斯特属于惜字如金的那个类别,但与高斯和怀尔斯不同,他喜欢在发表的论文中提及他已经得到的结果,承诺会写出相关的论文,但这个承诺却迟迟不见兑现的踪影。在他发表的这篇摘要里,他除了提到上述超穷的层级结构之外,还提示了更多的结果。也许波斯特是想吊一下别的数学家的胃口,但对于同样在这个领域工作的人,这很不公平。如果你也是研究这个方向的学者,你读了波斯特的这篇文章,可能希望在这些结论上生发出更深入的定理。但因为这些结论的证明并没有正式发表,你并不知道波斯特的这些结论到底是有凭有据,还是仅仅是虚张声势,从而陷入想用但没法用的两难境地。更糟糕的是,如果你发现了相同的结论,希望发表的话,又会出现优先权之争,而这是大家都不希望看到的。无论如何,仅仅提示结果而长久拖延正式论文的发表,对学术整体的发展相当不利。
克林对波斯特这篇摘要的意见也正在于此。他给波斯特写了一封信,除了赞扬他的结果以及一些讨论之外,还提及了不发表的这个问题。克林的信也许使波斯特的良心有些不安,他很快给克林寄去了一份包含他的新结果的手稿。这份手稿延续着波斯特一直以来的风格:依赖直觉,不太严谨,结构也很凌乱。因为这是一份手稿,混乱程度更甚。波斯特自己可能也知道这一点,他给克林的建议是:找个研究生,让他把内容整理出来,然后以合作者的身份一起发表这篇文章。克林依计行事,但这份手稿实在是太难理解,克林找来的研究生实在无能为力,最后克林只好捋起袖子自己动手。
克林是丘奇的学生,也继承了丘奇的那种追求严谨的研究风格。当年丘奇对严谨性的要求曾经让更依赖直觉的图灵吃了不少苦头,这次轮到克林被波斯特的手稿中的各种直觉描述所困扰了。但最终,克林还是将手稿中的内容整理出来,将缺少的证明补齐,并且做了一些延伸的研究,最后写成了一篇论文:
《递归不可解度的上半格》(The upper semi-lattice of degrees of recursive unsolvability)。
所谓的“递归不可解度”,其实就是不可计算的那些图灵度。而“上半格”是一种序结构。波斯特与克林证明了,所有图灵度其实组成了一个非常复杂但有序的结构。我们此前看到,通过图灵跳跃得到的图灵度层级与算术层级关系非常密切,但与算术层级不同的是,在每个图灵度层级之间,还有更加令人惊讶的结构存在,也就是说,阶梯与阶梯之间并不是空无一物,还有更多的结构蕴含其中。这也是显然的,因为自然数的子集有不可数无穷个,但每个图灵度中最多包含可数个子集。所以,图灵度的个数是不可数的,比我们想象中的无穷还要多得多。图灵度层级必然不能概括所有图灵度的结构,那么,必然有更多的结构存在于层级之间。
假设

这篇论文,最终发表在久负盛名的《数学年刊》(Annals of Mathematics)上。可以说,它开创了图灵度研究这个新领域。到现在,图灵度理论已经成为了数理逻辑中非常活跃的一门分支,而其中主要的研究方法——被称为“优先方法”——它的一种雏形同样起源于这篇文章。
这就是作为数学家的波斯特,他的数学研究的顶峰。
