人算不如天算:之微分方程,分子,有限差分方法

田野中有一朵蒲公英,你向它吹了一口气,它的种子便随着你的气流在空中飞舞。于你而言,这只是一阵风,但对于自然而言,它又给出了一个偏微分方程的数值解。
流体问题
像水和空气这样会流动的东西,我们将它们称为流体。对流体的研究,肇源于古希腊阿基米德的浮力原理,经过十八世纪两位数学巨擎——欧拉和伯努利——的推动,最终在十九世纪达到顶峰。十九世纪的两位物理学家——纳维和斯托克斯——将流体流动的奥秘都汇聚到了一个偏微分方程中(注1)。这个方程也因他们而得名“纳维-斯托克斯方程”。
但随着实验水平的提高,人们发现,对于一些在极端条件之下的流体,纳维-斯托克斯方程失去了预言的力量。
究其原因,物理学家在研究流体的时候,假定流体是连续的,这与生活中的体验也是一致的。但事实上,空气和水都是由大量分子组成的,只不过因为分子的数量太多体积太小,我们才不能意识到其实每一阵风都是由离散的大量分子组成的,反而认为它们是连续的、没有间断的。但在极端条件之下,分子的这种离散的特性变得突出,变得不再那么连续了。既然“流体是连续的”这个假设失效了,那么流体力学方程在极端条件下失去准确性也就并非不可理解了。
对于物理学家来说,这就意味着在极端条件下,他们需要从另外的假设出发来推导流体所服从的方程。但对于研究数学分析的数学家来说,连续的流体要比离散的原子分子更自然,方程比现实更自然。与其说方程描述了现实,不如说现实是方程的近似。在每一阵风中,自然给我们展示的,正是如何通过离散去得到连续。
风是空气的流动,虽然空气是由一个个离散的分子组成的,但由于分子体积极小而数量惊人,在我们看来,空气就变成连续的了,于是风——空气的流动——也就是连续的。这就跟那些大型的广告一样:在远处看,广告上是一位天真无邪的小孩子,但靠近看的话,不过是数量巨大的油墨点组成的点阵而已。
自然告诉我们的,正是这样一个道理:通过离散的手段,也能模拟出连续的现象。
话分两头,为了模拟流体的流动,研究人员发展了一种数值计算方法,它叫有限差分方法,能给出一些偏微分方程的数值解。而有限差分方法的精髓,正是自然告诉我们的道理:通过离散的手段,模拟连续的现象。
它将一个原本连续的区域离散化,划分成一个一个的点,就像空气中的分子。然后它将要求解的问题翻译成线性方程组,也就是说将连续的问题转化为离散的问题。最后通过求解这个方程组,它就得到了原来问题的一个数值解。由于计算机善于处理离散的问题,而离散的问题也会比连续的容易处理,这就使有限差分方法成为了得到偏微分方程的近似数值解的好工具。
我们来看一个用有限差分方法解决问题的例子。
数学模型
【公式出没,注意!不适者欢迎绕行。相信我,不会过于影响后面的阅读。】
如果我们将下面这个铁丝架浸到肥皂水中再拿出来,架上会有一层肥皂膜,它是什么形状的呢?
为了描绘肥皂膜的形状,我们可以将这个架子放在一个平面上,然后肥皂膜作为一个曲面,就可以用一个定义在 [0,1]*[0,1] 这个正方形上的函数f来描述了。(细黑线是等高线)
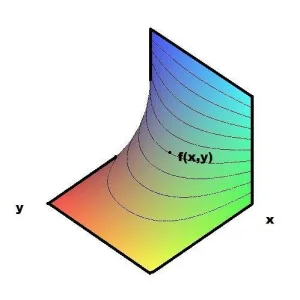
而在这个正方形的边界上,由于肥皂泡附着在架子上,所以在一条边上,函数f的取值为1,而在其它边上它的取值为0。这种定义在边界上的条件被数学家称为边界条件。
由于表面张力的原因,从局部看来,肥皂膜肯定是非常平滑的。任何可能的突起都会迅速被表面张力拉平。如果将这种平滑的特性翻译成数学的语言的话,就是函数 f满足以下偏微分方程:
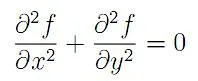
于是,我们需要解决的问题就变成:在正方形 [0,1]*[0,1] 内,根据给定的边界条件,数值求解以上的偏微分方程。
这正是有限差分方法派上用场的时候。
有限差分方法的回答
不知道有限差分方法的灵感是否来自自然,但以自然作类比,我们能更好地理解它。
回到肥皂膜的例子上,我们知道,实际上肥皂膜并不是连续的,而是由数量有限的水分子和肥皂分子构成的,它的整体形状也是由这些分子的相互作用所决定的。如果我们能够在计算机上模拟肥皂膜上每个分子和它们的相互作用的话,我们就能得到整个肥皂膜的形状。
但尽管这些分子的数量有限,对于现代计算机而言仍是天文数字,完全的模拟并不可行。是否可能减少进行模拟的分子数量,牺牲模拟的精度去换取更高的速度呢?不妨想象一下,如果肥皂的分子很大很大,大到那块肥皂膜变成一个16×16的分子网格,上面只有256个“肥皂分子”。那么,由于需要模拟的分子数目不大,对肥皂膜的模拟变得非常容易。
不妨试试在这种基础上做个模拟,看看结果如何。
我们不妨假定这些巨大的“肥皂分子”在平面上的投影将正方形分成了一个16×16的网格。
每个格点都代表了一个“肥皂分子”。那么,只要知道每个格点对应的“肥皂分子”离地面的高度,我们就能知道整个肥皂膜的形状了。我们用
然后,我们需要将刚才的偏微分方程表达成这些
用自然语言来说,就是一个“肥皂分子”的高度正好是它前后左右四位邻居高度的平均值。这也非常符合我们的直觉,因为只有这样,在每个局部看来这个肥皂膜都是比较平坦的。如果我们想象每个“肥皂分子”的邻居都用同样大小的力(可以看作表面张力)拉着它的话,它的稳定位置正好就符合上面的方程。
数学家们把这个关系成为偏微分方程的差分形式,这也就是“有限差分方法”这个名字的来源。
最后剩下的要翻译过来的内容就是边界条件了。在网格的边界处,“肥皂分子”都是附着在铁丝网上的。根据铁丝网的形状,我们容易知道,除了网格第一行的“肥皂分子”的离地高度都是1以外,其余的都是0。
当所有条件都翻译完毕后,我们手头上就有了一个由这些条件构成的线性方程组。剩下的工作就是解方程组。对于计算机来说这是小菜一碟。将方程组的解画出来,就是这样:
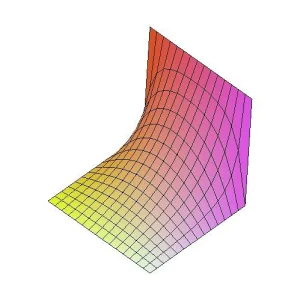
效果似乎不错,但正确性如何呢?
我们同时画出原来偏微分方程的解:
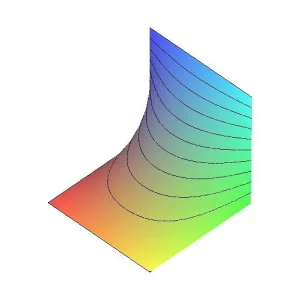
肉眼看不出它们之间的差异,不是吗?
事实上,有限差分方法得出的解是一个比较好的近似,而它所需要的计算资源也不多。对于经常处理边界复杂的偏微分方程的工程师而言,这些问题如果用传统的数学分析方法解决的话,计算量相当浩大,只能人手计算,更别提需要做的各种近似了;但如果利用有限元方法的话,误差不算太大,计算量却不太大,而且可以交给计算机去处理。
从上面的例子中,我们可以窥见有限差分方法的一般框架:对于一个求偏微分方程解的问题,先将要求解的区域剖分成网格,然后将偏微分方程和边界条件翻译成网格中每一个格点之间的关系,从而得到一个多变量的方程组,每一个格点对应一个变量,最后通过求解这个方程组,我们得到一组解,结合原来的网格,我们就得到了原来问题的一个数值解。
自然的总结
流体力学研究的自然流体实际上是离散的分子组成的,我们不知道有限差分方法的灵感是否来源于此,但它的确曾在计算流体力学中起过很大的作用。它也被应用在热力学的数值计算中。它的吸引力很大一部分来源于它的简单和易用。
但有限差分方法也并非尽善尽美。它的求解过程只能在一个形状规则、分布均匀的网格上进行,但显然会有某些地方的变化更值得关注。比如说,如果我们想要模拟一条溪流,我们肯定更关注礁石丛生之处被扰乱的水流,而不是毫无阻碍缓缓流淌的部分。而有限差分方法对模拟区域是一视同仁的,每个地方的模拟精度都是一样的,这样的话为了提高精度,很多计算资源就被白白浪费在无关紧要的地方上。除此之外,还有精度和数值稳定性的问题。
通过对有限差分方法的改进,人们可以部分地绕过这些问题。也有别的数值计算方法可以弥补这些缺陷,如有限元方法、有限体积方法等。它们的基本思路与有限差分方法是一样的:将问题用不同的方式离散化,然后用离散的手段去解决它。
而这,正是由分子和原子组成的每一股水流、每一阵风每时每刻都在做的事情,而且它们比我们、比计算机做得更好。这就是自然在计算,它是一个巨大的并行计算机。它以不计其数的分子和原子,用离散的方法,编织了一个连续的世界;我们活在其中,却不自觉。

注1:纳维-斯托克斯方程看起来是这样的:
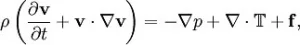
自然用原子和分子就能模拟出如此复杂的偏微分方程,着实令人惊叹。